云之南

欧氏距离：（∑（Xi-Yi）2）1/2，即两项间的差是每个变量值差的平方和再平方根，目的是计算其间的整体距离

即不相似性。

我们熟悉的欧氏距离虽然很有用，但也有明显的缺点。它将样品的不同属性（即各指标或各变量）之间的差别等

同看待，这一点有时不能满足实际要求。例如，在教育研究中，经常遇到对人的分析和判别，个体的不同属性对

于区分个体有着不同的重要性。因此，有时需要采用不同的距离函数。

如果用dij表示第i个样品和第j个样品之间的距离，那么对一切i，j和k，dij应该满足如下四个条件：

①当且仅当i=j时，dij=0

②dij＞0

③dij＝dji（对称性）

④dij≤dik＋dkj（三角不等式）

显然，欧氏距离满足以上四个条件。满足以上条件的函数有多种，本节将要用到的马氏距离也是其中的一种。

第i个样品与第j个样品的马氏距离dij用下式计算：

dij=(xi一xj)'S-1(xi一xj)

其中，xi和xj分别为第i个和第j个样品的m个指标所组成的向量，S为样本协方差矩阵。

马氏距离有很多优点。它不受量纲的影响，两点之间的马氏距离与原始数据的测量单位无关；由标准化数据和中

心化数据(即原始数据与均值之差）计算出的二点之间的马氏距离相同。马氏距离还可以排除变量之间的相关性的

干扰。它的缺点是夸大了变化微小的变量的作用。

In statistics, the Bhattacharyya distance measures the similarity of two discrete probability distributions. It is normally used to measure the separability of classes in classification.

For discrete probability distributions p and q over the same domain X, it is defined as: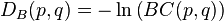

where: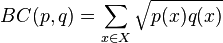

is the Bhattacharyya coefficient. For continuous distributions, the Bhattacharyya coefficient is defined as: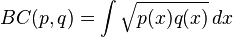

In either case, and 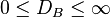. DB need not obey the triangle inequality, but does obey the triangle inequality.

For multivariate Gaussian distributions pi = N(mi,Pi),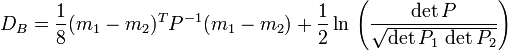

,

where mi and Pi are the means and covariances of the distributions, and

.

Note that the first term in the Bhattacharyya distance is related to the Mahalanobis distance.（巴式距离和马氏距离之间的关系）